Lambda Calculus
How mathematical theories continue to influence modern development
Disclaimer: Our Tech Blog is a showcase of the amazing talent and personal interests of our team. While the content is reviewed for accuracy, each article is a personal expression of their interests and reflects their unique style. Welcome to our playground!
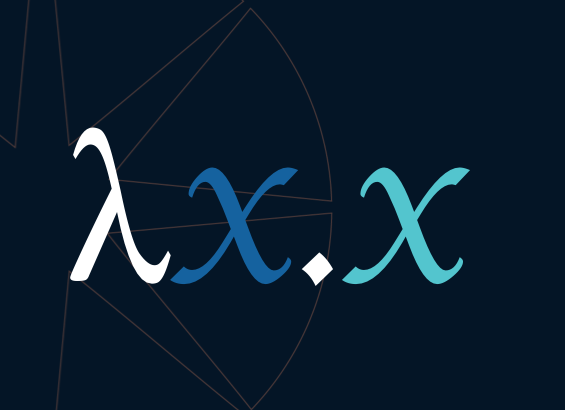
Lambda Calculus
From my recent BreviTalk on the Lambda Calculus
I recently gave a BreviTalk at my company on lambda calculus and its connection to modern JavaScript development. I really enjoyed exploring this topic in depth and presenting it to my fellow Sparkers. Therefore, I decided to write an article as well, so that more people can learn about these concepts.
Most developers use functional programming concepts daily without knowing where they come from. Array methods like map and filter, React hooks, Redux reducers, they all trace back to this mathematical theory, the Lambda Calculus.
The Two Computational Models
In 1930, mathematician Alonzo Church started developing the lambda calculus, asking whether all computation could be expressed through mathematical functions. Around the same time, Alan Turing was working on his machine concept, the foundation of modern computers.
Turing later proved these approaches were equivalent. Anything computable with one method also works with the other. But here’s the thing: the software industry mostly followed Turing’s path, building layer upon layer of abstractions to manage memory, state, and side effects.
What if we’d gone the other direction?
Lambda Calculus: Three Simple Rules
Lambda calculus, in its pure form, has exactly three building blocks:
- Variables: Placeholders like
xory - Abstractions: Functions written as
λx.x(take input x, return what follows the dot, x in this case) - Applications: Applying functions to arguments
(f x)
That’s it. No built-in operators, no if statements, no loops. Just functions.
Reduction Operations
Lambda calculus has two fundamental operations for manipulating expressions:
Alpha Conversion
This allows us to rename bound variables to avoid conflicts. Variable names don’t matter, only the binding structure does.
For example: λx.x is equivalent to λy.y (both are the identity function)
This is crucial when we need to avoid variable capture during substitution.
Beta Reduction
This is how we “execute” lambda expressions by substituting arguments into functions.
When we have an application like (λx.M) N, we reduce it by:
- Taking the function
λx.M - Substituting every occurrence of
xinMwithN - Returning the result
For example: (λx.x) y reduces to y (the identity function applied to y returns y).
These two simple operations are all we need to perform computation in lambda calculus.
Building Everything from Basic Combinators
In pure lambda calculus, we must distinguish between free and bound variables to avoid variable capture, when a free variable accidentally gets bound by a lambda abstraction during substitution. To sidestep these complications entirely, we can work with combinators: functions that contain no free variables and are completely self-contained. This is where lambda calculus gets really interesting.
The Foundation: K and I Combinators
// K Combinator (Kestrel) Always returns the first argument
const K = (x) => (y) => x;
// I Combinator (Identity) Returns whatever you give it
const I = (x) => x;
These might look simple, but they’re incredibly powerful. Let’s see how we can derive more complex behavior from these basics.
Deriving the KI Combinator
Here’s something cool I demonstrated during my talk. We can actually derive a new combinator from existing ones:
// KI Combinator Always returns the second argument
let KI = (x) => (y) => y;
// But we can also derive it as:
KI = K(I);
// Why does this work? Let's trace through it:
// K(I)(x)(y) = I(y) = y
// So K(I) behaves exactly like our KI combinator!
All existing combinators can be derived from the fundamental K, I, and S combinators.
const S = (f) => (g) => (x) => f(x)(g(x));
Building Boolean Logic from Nothing
In pure lambda calculus, there are no boolean values. So how do you represent true and false? You use the combinators we just built!
Think: we have a function that needs to choose between two options.
The key insight is that booleans are selectors:
- True always picks the first option:
λx.λy.x(this is the K combinator!) - False always picks the second option:
λx.λy.y(this is the KI combinator!)
// Booleans are just selection functions
const TRUE = K; // Select first argument
const FALSE = KI; // Select second argument
// Test them out
console.log(TRUE("first")("second")); // Returns "first"
console.log(FALSE("first")("second")); // Returns "second"
Now we can build logical operations:
// NOT flips the selection by offering opposite choices
const NOT = (p) => p(FALSE)(TRUE);
// AND: if first is true, return second; otherwise false
const AND = (p) => (q) => p(q)(FALSE);
// OR: if first is true, return true; otherwise return second
const OR = (p) => (q) => p(TRUE)(q);
Let me show you how this works in practice:
// Testing our boolean logic
console.log("NOT(TRUE):", NOT(TRUE) === FALSE); // true
console.log("NOT(FALSE):", NOT(FALSE) === TRUE); // true
// AND logic
console.log("TRUE AND TRUE:", AND(TRUE)(TRUE) === TRUE); // true
console.log("TRUE AND FALSE:", AND(TRUE)(FALSE) === FALSE); // true
console.log("FALSE AND TRUE:", AND(FALSE)(TRUE) === FALSE); // true
The Cardinal Combinator: An Alternative to NOT
There’s an even more elegant way to implement negation using the Cardinal combinator:
// C Combinator (Cardinal) Flips the order of arguments
const C = (f) => (x) => (y) => f(y)(x);
// Cardinal can serve as NOT by flipping the arguments!
// C(TRUE)('a')('b') returns 'b' (acts like FALSE)
// C(FALSE)('a')('b') returns 'a' (acts like TRUE)
// We can prove they're equivalent
const testEquivalence = (f, g) => {
const a = "first",
b = "second";
return f(a)(b) === g(a)(b);
};
console.log("C(TRUE) ≡ FALSE:", testEquivalence(C(TRUE), FALSE)); // true
console.log("C(FALSE) ≡ TRUE:", testEquivalence(C(FALSE), TRUE)); // true
“Real-World” Applications
For my talk, I built a football team management system using these principles:
Team Selection Logic
const team = [
{
name: "Roy Kent",
position: "midfielder",
skill: 95,
fitness: 70,
salary: 80000,
},
{
name: "Jamie Tartt",
position: "striker",
skill: 90,
fitness: 85,
salary: 120000,
},
{
name: "Sam Obisanya",
position: "defender",
skill: 85,
fitness: 95,
salary: 40000,
},
];
// Convert regular booleans to our lambda booleans
const isSkilled = (player) => (player.skill >= 80 ? TRUE : FALSE);
const isFit = (player) => (player.fitness >= 80 ? TRUE : FALSE);
const isAffordable = (player) => (player.salary <= 70000 ? TRUE : FALSE);
// Complex selection logic using our combinators
const canStartMatch = (player) => {
const skilled = isSkilled(player);
const fit = isFit(player);
return AND(skilled)(fit)("STARTER")("BENCH");
};
const isGoodValue = (player) => {
const skilled = isSkilled(player);
const affordable = isAffordable(player);
return OR(skilled)(affordable)("GOOD_VALUE")("EXPENSIVE");
};
// Apply to our team
team.forEach((player) => {
const matchStatus = canStartMatch(player);
const valueStatus = isGoodValue(player);
console.log(`${player.name}: ${matchStatus}, ${valueStatus}`);
});
Immutable Configuration (K Combinator)
// Use K combinator for configuration that can't be modified
const createConfig = K;
const gameConfig = {
maxPlayersOnField: createConfig(11),
matchDuration: createConfig(90),
budgetLimit: createConfig(1000000),
};
// Try to override it won't work!
console.log("Max players:", gameConfig.maxPlayersOnField(999)); // Still returns 11
console.log("Budget limit:", gameConfig.budgetLimit(500000)); // Still returns 1000000
Data Validation (Identity Combinator)
// I combinator for clean data validation
const validatePlayer = (player) => {
const isValid = player.skill > 0 && player.fitness > 0 && player.salary > 0;
return isValid ? I(player) : FALSE;
};
const validateTeam = (players) => players.map(validatePlayer);
console.log(
"Valid players:",
validateTeam(team).filter((p) => p !== FALSE).length
);
Default Value Handling (KI Combinator)
// Use our boolean system for graceful defaults
const getPlayerValue = (player, attribute) => {
const hasAttribute = player[attribute] !== undefined;
const selector = hasAttribute ? TRUE : FALSE;
return selector(player[attribute])("Unknown");
};
team.forEach((player) => {
const position = getPlayerValue(player, "position");
const nationality = getPlayerValue(player, "nationality"); // Missing attribute
console.log(`${player.name}: ${position}, Nationality: ${nationality}`);
});
Why This Matters for JavaScript Developers
Lambda calculus principles are everywhere in modern JavaScript:
- React hooks manage state through pure functions
- Array methods like
mapandfilterare function composition - Redux reducers must be pure functions
- Functional components eliminate class based side effects
When you embrace pure functions (no side effects, same input always produces same output), you get:
- Predictable code that’s easier to test
- Better debugging (problems are isolated)
- Safer concurrency (no shared state conflicts)
- More composable, reusable functions
Practical Takeaways
You don’t need to rewrite everything, but even small changes make a difference:
// Instead of mutating objects
function updatePlayer(player, newSkill) {
player.skill = newSkill; // Mutates original
return player;
}
// Return new objects
function updatePlayer(player, newSkill) {
return { ...player, skill: newSkill }; // Pure function
}
Keep functions small, avoid shared state, make dependencies explicit through parameters.
The Bigger Picture
Church’s lambda calculus teaches us something important: elegant solutions often come from simple building blocks. The same three concepts variables, functions, and applications can express any computation.
Modern JavaScript development is moving toward these principles. Understanding where they come from helps you write better code.
Lambda calculus isn’t just academic theory. It’s a practical approach to building more reliable software. The 1930s math still works because the problems it solves (complexity, unpredictability, side effects) haven’t changed.
